Math is a cool way for us to understand the world we live in. And to that end Business Insider recently spoke with Steven Strogatz , the Jacob Gould Schurman Professor of Applied Mathematics at Cornell University.
Strogatz specializes in areas of nonlinear dynamics and complex systems, and he is the author of the wonderful “Joy of X: A Guided Tour of Math, from One to Infinity.”
He talked to us about game theory, “elegant” math, math education, and the effectiveness of models in different fields.
This interview has been edited for clarity and length. It was originally published on June 8, 2016.
Elena Holodny: What's interesting in chaos theory right now?
Steven Strogatz: I'm often very interested in whatever my students get interested in. I primarily think of myself as a teacher and a guide. I try to help them - especially my Ph.D. students - become the mathematicians they're trying to become. The answer often depends on what they want to do.
In broad terms, the question of how order emerges out of chaos. Even though we talk about it as "chaos theory," I'm really more interested in the orderly side of nature than the chaotic side. And I love the idea that things can organize themselves. Whether those things are our system of morality or our universe or our bodies as we grow from a single cell to the people we eventually become. All this kind of unfolding of structure and organization all around us and inside of us, to me, is inspiring and baffling. I live for that kind of thing, to try to understand where these patterns come from.
Holodny: How do things organize themselves in nature even when there's no "central command" - like when birds fly in formation or people organize themselves in a power structure?
Strogatz: We're learning a lot about this all the time - bird flocks, fish schools, herds of animals. You can have human organization both within companies or even frivolous examples like people in a soccer match who want to start doing the wave or clapping in unison. So we do sometimes spontaneously organize.
There are also cases when it's really serious, like when buildings are on fire and people need to escape. You can study the motion of people as they escape the building. And they actually will go out like water flowing through a pipe … There's a kind of "fluid dynamics of people" as well as of cars. When traffic engineers are trying to figure out how people are driving ... sometimes you'll be stuck in traffic and there's a jam, and you're thinking, "Oh there must be an accident somewhere down the road," but then you never see an accident and you wonder why was there this traffic jam? There was no reason for this.

So that's another case of bizarre collective behavior of people that we get in these density waves on the highway. Density of traffic in some places and density somewhere else. And in that case it has to do with driver behavior. That people don't want to get too close to the car in front of them. There are sort of mathematical rules that govern how fast you're comfortable driving, depending on how far ahead of you the next car is, and also how dense the traffic is generally. And so you can write all of these things in math and then start to predict what will happen with thousands of people on a big long stretch of highway.
Or in the case of birds. They are flying around in three dimensions, and they're very aware of how close their neighbors are, how fast the neighbors are going, which directions the neighbors are pointing. They don't have eyes on the backs of their heads, so they're not so aware of who's behind them.
But, like I said, there are simple rules about what a bird will do in response to a neighboring birds based on how fast they're going, how close they are, and which directions they're pointing. And then if you make computer simulations of what you'd expect, each bird is following these simple rules. You get behavior that looks exactly like what real flocks look like, including if they're flying around obstacles such as buildings or trees. You don't need a leader.
Holodny: To what degree are these computer simulations accurate? We don't even know how to solve turbulence yet!
Strogatz: [Laughs] Well, that's true. But turbulence is much harder than bird flocks, I would say. Because we can make measurements on individual birds. You can have them follow robotic birds; you can train them. You can kind of directly measure some of their response properties to other birds of their same species.
I don't want to give the impression that we totally understand flocks. You're right to be skeptical. There's a lot that we're just learning about this, but the field seems to be moving pretty fast.
Holodny: What do you mean by "the organization of morality"?
Strogatz: Yes, that's a strange phrase. The reason I said that is - maybe you're familiar with game theory and the prisoner's dilemma?
I'm thinking here of this incredible computer study that was organized by a political scientist called Robert Axelrod. … In the 1980s, he asked the world's leading game theorists from psychology and economics and computer science - all kinds of different disciplines - to submit computer programs to play prisoner's dilemma against each other ... It was a repeated prisoner's dilemma. Everybody played everyone many times … And the question was, "What would do well in the kind of environment where everyone is using all of these different strategies?"
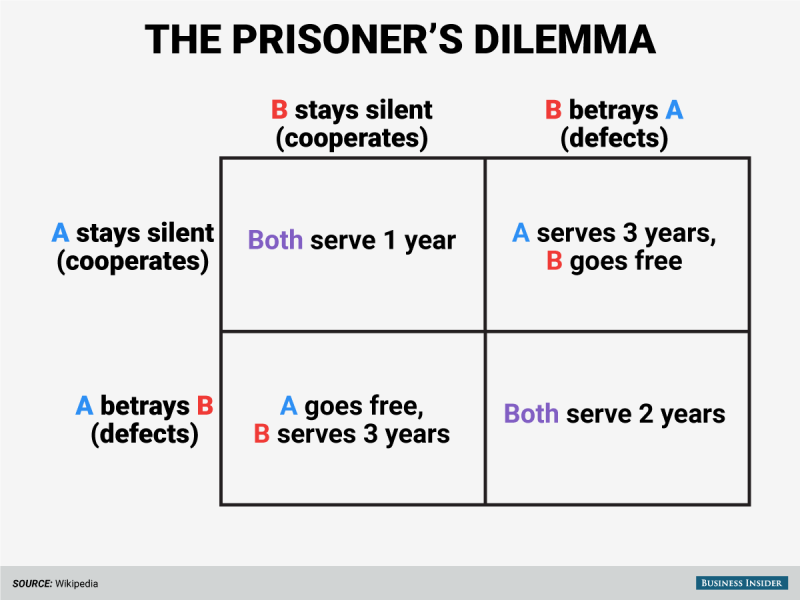
What this showed was that the winning strategy was the strategy that people called "tit for tat." It begins by cooperating on the first move and then does whatever the opponent did. So if the opponent cheated, or "defected" as they say, then they will defect in retaliation. And so it's a very simple strategy - it was actually the shortest program that was submitted to the tournament. Only four lines of FORTRAN, the computer language of the era in 1980. So it was the shortest program, and was very simple-minded, but it ended up winning.
Keep in mind here: These programs are not trying to be goody two-shoes. They're trying to win. These are self-interested individuals. These are egoists, these are free market people, they're capitalists, they're try to do anything to win. So there's no sense of morality here. This is just "What does it take to win?"
Now, to come to the punch line, when Axelrod analyzed what programs tended to do well in this prisoner's dilemma tournament, the ones that did well had four properties: Be nice, be provocable, be forgiving, and be clear. [Editor's note: "Nice" means to cooperate; "provocable" means to immediately defect in retaliation when the other player defects on you; "forgiving" means not to hold a grudge, e.g., someone resumes cooperating with you, and then you resume cooperating and don't continue to punish them.]
So what emerged from the prisoner's dilemma tournament was be nice, provocable, forgiving, and clear, which to me sounds a lot like the ancient morality that you find in many cultures around the world. This is the "eye for an eye" morality, stern justice. This is not the New Testament, by the way. This is the Old Testament. And I'm not saying it's necessarily right; I'm just saying it's interesting that it emerged - it self-organized - into this state of being that the Old Testament morality ended up winning in this environment.

There's a footnote to this story that's really interesting, which is that after Axelrod did this work in the early 1980s, a lot of people thought, "Well, you know, that's it. The best thing to do is to play 'tit for tat.'" But it turns out it's not so simple. Of course nothing is ever so simple. His tournament made a certain unrealistic assumption, which was that everybody had perfect information about what everybody did, that nobody ever misunderstands each other. And that's a problem, because in real life somebody might cooperate, but because of a misunderstanding you might think that they defected. You might feel insulted by their behavior, even though they were trying to be nice. That happens all the time.
Or, similarly, someone might try to be nice, and they accidentally slip up, and they do something offensive. That happens, too. So you can have errors … watch what happens, if you have two "tit for tat" players playing each other, and everybody is following the Old Testament, but then someone misunderstands someone else, well, then watch what happens. Someone says, "Hey, you just insulted me. Now I have to retaliate." And then, "Well, now that you've retaliated I have to retaliate because I play by the same code." And now we're stuck in this vendetta where we're alternating punishing each other for a very long time - which might remind you of some of the conflicts around the world where one side says, "Well, we're just getting you back for what you did." And this can go on for a long time.
But you could say morality came from evolution - it's natural selection, which is all we're talking about here - trying to win at the game of life. If natural selection leads to morality, I think that's pretty interesting. And that came from math!
So in fact what was found in later studies, when they examined prisoner's dilemma in environments where errors occurred with a certain frequency, is that the population tended to evolve to more generous, more like New Testament strategies that will "turn the other cheek." And would take a certain amount of unprovoked bad behavior by the opponent ... just in order to avoid getting into these sort of vendettas. So you find the evolution of more gradually more and more generous strategies, which I think is interesting that the Old Testament sort of naturally led to the New Testament in the computer tournament - with no one teaching it to do so.
And finally, this is the ultimately disturbing part, is once the world evolves to place where everybody is playing very "Jesus-like" strategies, that opens the door for the [the player who always defects] to come back. Everyone is so nice - and they take advantage of that.
I mean, the one thing that's really good about "tit for tat" is that … the player who always defects - he can't make much progress against "tit for tat." But it can against the very soft, always cooperating strategies. You end up getting into these extremely long cycles going from all defection to "tit for tat" to always cooperate and back to all defection. Which sort of sounds a lot like some stories you might have heard in history. Countries or civilizations getting softer and softer and then they get taken over by the barbarians.
So anyway, I mean, it's all just stories. But what I meant when I said "morality is self-organizing" - because it's an interesting question for history: where does morality come from? And you might say morality came from God - OK, that's one kind of answer. But you could say morality came from evolution; it's natural selection, which is all we're talking about here, trying to win at the game of life. If natural selection leads to morality, that's pretty interesting. And that came from math!
Holodny: So in a painting, for example, a line is something in it of itself but also expresses something else, an approximation of what we see in reality. It seems like math has that as well, with six as a concept, but then you have a measurement of six inches. But measurements are imprecise, so in that way it's not accurate but rather an approximate reflection of reality. Is there a direction that the math world is moving in here?
Strogatz: Well, this is one of the oldest questions there is. I wouldn't say that this is a recent development or moving in any direction. This goes very far back.
Holodny: This is like Plato versus Aristotle.
Strogatz: Exactly. This is Plato, man! You know, where do these concepts live? Because for him, there's the triangle you can draw in the sand, and then there's the triangle that exists in the world of pure ideas - the Platonic realm, whatever that means. It sounds like nonsense, because there is no such place. Where is that place? Yet, it's very helpful to imagine that there is such a thing as a perfect equilateral triangle or a perfect circle.
It sort of seems like our math can't possibly be compatible with reality. Except that it is! And not just compatible, but remarkably powerful.
Take a real number, say, the number pi, which kids always find kind of baffling because they like to start reciting the digits ... It looks kind of random. 3.14592 … So there's no simple sequence here except that these are the digits of pi. But if I tell you that there are infinitely many digits of pi - it never ends, it never repeats, it goes on with no pattern that we can discern - and that's what a typical number looks like. That's a very bizarre abstraction because in the real world, nothing is infinite as far as we know. And what's so amazing is that we have all kinds of reasoning about such things - going back to Euclid, and Plato, and Pythagoras. We get conclusions, as well as more high-powered things about calculus with the concept of real numbers.
Quantum theory would tell us that there's only a finite number of particles in the universe. The universe is not thought to be of infinite size. We're not sure but, you know. So, infinity, I think you can make a pretty good case that there is no infinity in the real world. And yet, even to describe basic numbers like pi, you need to the concept of infinity. And so it sort of seems like our math can't possibly be compatible with reality. Except that it is! And not just compatible, but remarkably powerful.
It's this spooky thing where you reason about perfect objects, like real numbers or perfect circles or equilateral triangles - we know that they don't really exist, and yet by pretending that they do exist to a good approximation in the real world, you get predictions that work.
It's given us the phone that we're talking on right now. The electricity and magnetism that let people predict that you can do wireless communication, and then turns out you can make gadgets that do it. That came out of studying a subject called vector calculus that Maxwell did in the late 1800s. That prediction of wireless, or rather, the real prediction was that electricity and magnetism together could make a wave that would move at the speed of light that's an electromagnetic wave is what radio waves are - that was the prediction. No one knew that that was the case; it came out of math. And then it was measured, and it was exactly right.
So it's this spooky thing where you reason about perfect objects, like real numbers or perfect circles or equilateral triangles - we know that they don't really exist, and yet by pretending that they do exist to a good approximation in the real world, you get predictions that work.
At least in physics. It's not as good in biology, and it's even less good in psychology and economics, as you know well. [Laughs]
Some things are very well described by math and others are still in the future to be better described by math - or maybe in principle they can't be - we don't know in some cases. I mean like, it could be that the irrationality of people is just beyond mathematical description and that's why we have so much trouble in subjects where human beings are the dominant force. But we'll see. We don't know. We're working hard.
Holodny: It's fascinating how much of a difference there is between physics math and economics math. Econometric models, already at the start, seem to me to be "inaccurate" because they were biased toward a person's opinion.
Strogatz: Yeah, that's a good point. I mean, what's the right scientific model for economics? Is it physics? Like some of the early practitioners of economics seem to talk about equilibrium - and you'd see in the old days of Keynesian economics ... people making models with "pressure." They even built hydraulic computers to try to compute the flows in the economy. They took it very literally as flows of money, except they pretended it was water.
So there was that, but nowadays a lot of people think that biology is the better model for economics.
Holodny: Angus Deaton, who won the 2015 Nobel Prize in economics, is more of a data collector by style, and that's more similar to biologists who look at the nitty-gritty details of a given population to predict what might happen next. As opposed to just building models, and then wondering why things in the real world don't look like your model.
Strogatz: But also you hear a lot about businesses replacing others through processes of creative destruction. And that there's an ecosystem of companies and interacting with the government. Also with weather and all kinds of stuff. And there's a whole complicated, really, ecosystem, and that seems to be the picture - with a lot of Darwinian competition and cooperation.
So maybe it's true that biology gives us a better analogy than physics. But there are some things - even with biology - that are governed by physics, too. You can't really escape the laws of nature, meaning, the laws of physics and chemistry. I don't think it's an either/or. Those physics and chemistry principles go very deep, reflecting even in the functioning of people, cities, and economies.
Holodny: Let's go in a different direction. Many people say math is boring.
Strogatz: I get the point about why people find math boring or "meaningless." I have two daughters - one's in high school and the other just finished middle school - and their teachers are trying to do their best. And they have a lot that they're supposed to teach according to the curriculum, the standards and all. There's a rush to teach students what they're supposed to know. And kids don't all go at the same pace, so some are left behind, others are bored. And also, often what they're teaching is often not what any kid would ask.

If I could say just one, simple thing, that would be it: much of school is about - and I don't just mean math, but school in general - is about teaching kids the answers to questions they're not asking. And that's kind of inherently boring. That is, if you're stuck at a party and someone is going on telling you something you don't have any interest in, and you would never ask about that, but they're just dumping the answers on you - that is the definition of boredom. [Laughs]
So I feel bad about that because the teachers are stuck: They're supposed to do what they're doing, but for many people it's automatically boring, whether it's history, or English, or math. But math is especially tough because there's a lot of jargon, a lot of unfamiliar ideas. It's difficult - it truly is ... People do have to concentrate, and a lot of people don't like to have to concentrate that hard for that long. There are certain things that are difficult about the subject.
But on the other hand, it is true that a lot of little kids like puzzles. That is, many people do like using their minds to solve logic puzzles or crossword puzzles or brain teasers. And you don't even have to be very smart to like that. I think a lot of people like that.
I'm kind of arguing against myself. Even though math can be difficult, so what? A lot of things can be difficult. It's difficult to shoot a basket from 20 feet away, but people like to practice and try to do it. Can't math be like that too? And the answer is, of course it can. And in the hands of a good teacher, it is like that.
It's difficult to shoot a basket from 20 feet away, but people like to practice and try to do it. Can't math be like that too? And the answer is, of course it can. And in the hands of a good teacher, it is like that.
That teacher could be a parent or an actual teacher. I think we've all had good teachers who inspired us to want to learn more math and helped us, and then we've also had some not-so-good teachers who started to turn us off. That's not really different from anything else because in any profession; there are good dentists and bad dentists.
But anyway, I guess as far as what to do about this, you have to hope that bright or creative people go into teaching and are rewarded for doing it … But it does make me feel bad, and of course all mathematicians feel bad, that so many people hate our subject. But it is a common experience, especially in America, to run into people who say, "Oh God - I hated math." Or, rather, what you frequently hear is "I was pretty good in math until we got to - " and then you'll hear decimals, or algebra, or geometry.
Holodny: What does it mean to you when a proof is "elegant" or "beautiful"?
Strogatz: I think elegant proofs or arguments or calculations all have a few features in common, which are that they tend to be concise - it's hard for something that's very long-winded to be "elegant" - so they're snappy and short usually. And they tend to be surprising; there's some kind of aha moment, you know, like you suddenly understand something but you didn't see it coming, so there's this combination of being surprising and yet inevitable that once you see the argument, that you see the proof, you feel like, "Oh that is really clear and obvious, I should've thought of that!"
Holodny: Do you think that describing math as beautiful could alienate people who don't immediately get it?
Strogatz: I worry about this a lot. If you keep talking about how it's beautiful, people who don't get the beauty may feel alienated or outside the club. It's worse. They already feel disempowered, and now it's like everyone else seems to get it and is enjoying it, and I feel left out. And that is not good, and I am sensitive to that. You're right, this obsession with the beauty of math, which we hear about is risky, double-edged.
A big part of teaching successfully is to have empathy. That you need to be sensitive to the students who aren't getting it, who don't see why it's beautiful.
A big part of teaching successfully is to have empathy. That you need to be sensitive to the students who aren't getting it, who don't see why it's beautiful. It's not beautiful to them if they're not getting it. The only remedy is to either help them get it, or to not keep harping on the beauty.
I have found that, when I ask my kids about when they like math - and, by the way, they don't always like it; I don't have two super-math-y children - they can do it, and they like to tease me about how much they hate it, but they don't really hate it. But when they seem happy with it, it's usually not because it's beautiful. I don't think it would even occur to them to say it's beautiful. What they like is that it's satisfying. That is just feels good that it works. It's satisfying that everything came out right. I don't know a better word for it than satisfaction: when the puzzle pieces fit, what does it feel like when you're done with a crossword puzzle or a jigsaw puzzle? You wouldn't call it beautiful. It's satisfaction, right? It's like a relief that, ah, yes, that worked. That's enough for many kids. You don't have to insist on "beauty" - which is a kind of a hoity-toity, pretentious thing in some circles.
The other aspect is that there's competition. Some kids - I want to say especially boys, but I don't know if that's correct - but there are definitely some kids that like beating other kids. And math gives them a very black-and-white way to beat them. You know, "I got a better score on this math test than my friend and I like that." And I have to admit that I felt that way. In seventh and eighth grade, I used to have a couple of friends who beat me in certain things… and I liked if I could beat them in math. [Laughs]
So, you know, we never talk about that when we talk about the popularization of math. It's a way you can beat someone. But it does give you that - if that's what you're looking for. There are competitive people out there.
Holodny: I totally relate to this.
Strogatz: Right, so I think beauty is one of the appealing aspects of math, but so is this - there's a kind of lack of subjective aspect to it. It can be very objective who solved the problem, who solved more problems, who did them better, simply, who got the higher score. And that's nice. In the same way that downhill ski racing doesn't have the same problems as figure skating has - where somebody is just faster. Whereas in figure skating, it depends on who the judges think showed more artistic merit. Some people don't like it when there are subjective things like art or beauty, and they would prefer pure speed, or I jumped higher, or I ran faster. Math definitely offers opportunities for that.
And actually, speaking of double-edged, that can be a turn-off for people, too. Because they see it as so black and white, they think math is cold or math doesn't leave room for creativity. But of course that's false because pretty much everything that human beings do leave room for creativity. And math is no different. An example would be when someone is solving a math problem; there's usually lots of different right ways to do it. And some will be more creative or more insightful than others. It's not true when people say that math is just right or wrong. You can have many things that are right, but some are more elegant or more creative or more insightful or illuminating than others.
And that's what we do at the higher levels of math; we're trying to be professional mathematicians. We're looking for proofs or calculations that illuminate, that make us have aha moments or feelings that we now understand something - down to the bottom of it. Rather than some ugly calculation that shows the answer, but we still don't understand why it works.
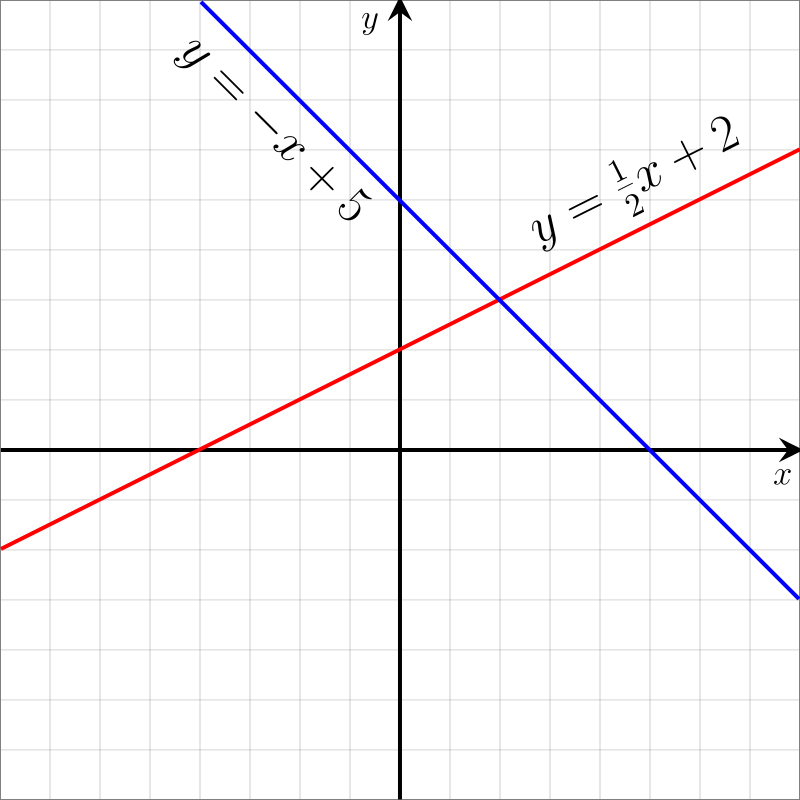
Another example of the aesthetic side of math is sometimes we'll find that two seemingly different parts of our subjects are connected. Like, we teach algebra and geometry separately, usually, but there's a thing called analytic geometry - or just to put it down to earth, when kids in high school learn y = mx+b as the equation for a line, they're connecting an algebra formula with the y's and x's to a geometric idea - the straight line. And then when they solve two equations simultaneously, that corresponds to the geometry of two lines crossing at a point. OK, that seems pretty easy … but human beings didn't know this until René Descartes and Pierre Fermat figured that out when they invented analytic geometry in the early 1600s.
So it's not like Pythagoras knew how to do this in 500 BC. I mean, it took 2,000 years for people to figure out this connection between algebra and geometry. That's kind of cool, too, isn't it? You can take a kid who's not so clever and teach them this technique in high school and they can learn to do it - solve simultaneous equations by making graphs of lines and looking where they cross - that defeats the best minds in the world from a few centuries earlier!
Holodny: Which is stunning.
Strogatz: It's amazing. These methods are so powerful. You can take the smartest people in the world at one time who couldn't understand and couldn't think of them, and then fast-forward 2000 years and now anybody can do it.

You don't even need to get as fancy as analytic geometry. Even arithmetic. People in ancient Rome could not really multiply because it's very hard to multiply Roman numerals. If you can remember them, with the X's and the V's and the L's. If you would try multiplying Roman numerals, it's quite tough. And so people in the street couldn't really do arithmetic, and they'd be counting on their fingers and stuff. Now, everybody can do arithmetic, and it's because in India they invented the concept of zero, which of course had to be invented. It wasn't there - the idea of nothing. People knew about "nothing," but they didn't know that it was a number. That was a big insight: that zero could be regarded as a number and that it would obey the same rules as the other numbers. And then of course negative numbers were invented, too.
So you have all these expansions of the universe of numbers that lead to greater and greater power and then ultimately this decimal system or writing the decimal point and then doing everything with base 10, which we don't even think about and just take for granted. But that's what they call Hindu-Arabic numbers. And the decimal system with place value - that came from India - and then through the Islamic world and eventually to Europe. And that was only in the 1200s. That this guy Fibonacci - who we always hear about with the Fibonacci numbers - he was the one who brought the Hindu-Arabic numbers to Europe, in Italy, and helped start the Renaissance. That took a few more hundred years, but still.
So, a lot of these things are kind of recent. We went a long time before arithmetic was common to the average person.
Holodny: What's your favorite course to teach?
Strogatz: That's a tricky one for me to answer. I do like them all. I did enjoy very much a course I taught a year ago, and will teach again next year, which is math for liberal-arts students. We call it "Mathematical Explorations," and the way that it's pitched is that this requirement that everyone has to take some quantitative reasoning. What you should be imagining here is the kid who really does not want to take math, and who thought, "Oh, God, I thought I was done with this in high school, and now my college is requiring me to take one more math course." These courses are designed for them. These are kids who don't take calculus. I mean, anyone who's doing calculus and is a science major, an economics major, they already passed out of this requirement. This is for everybody else.
What do you do in this course? Well, you could do something really boring - make them learn algebra again, which they didn't learn the first time. But what we did in the course was, first of all, no lectures. I didn't come up with this idea. This was developed at a college called Westfield State … "Discovering the Art of Math" is a course where they try to show the connections between math and art. Like dance or sculpture, the visual arts, music, everything. And not just art, but also literature, history … And I buy all this because sure, math is connected to all these things - but they really show it. For instance, if they want to teach the math in dance, they have the students - and I was following their approach - I would have my students get up and do … Well, a lot of kids are sensitive about dancing. So am I. I was a pretty lousy dancer. [Laughs] It's intimidating when someone says, OK, now we're going to do dance. What we would do is game where we were standing in front of each other, and I'd put up my left hand and you're facing me, and you have to look like my mirror image, so you'd put up your right hand. And then I start moving other parts of my body, and you're supposed to be doing the same as me but in mirror image.
What are we learning? We're learning about the concept of symmetry - the idea of a mirror reflection. And then I can do other types of symmetry, like instead of you being my mirror image, you could be me, but rotated 180 degrees … And so we start playing these games with symmetry, like we can add a third person. And so if you're 180 degrees rotate from me, but then the other person is a mirror image of you, then how is that different person related to me? And so you're composing symmetries, you're doing a symmetry of a symmetry. And what that gets to is the beginning of a subject called group theory, which is the study of symmetry that gets used in studying crystals or studying secret codes in cryptography or elementary particle physics. String theory is based on group theory. It's a really deep subject that we can illustrate by teaching these simple things about kids moving around and dancing.
It's a really different picture of a class - instead of everyone sitting and taking notes … I honestly think that it's the first time for many of these students that they've ever actually thought about mathematical things. Instead of memorizing or regurgitating on a test, they're actually thinking and solving problems and asking questions. It also has a whole emotional, psychological side to it, where I ask them to say what's confusing about this or what's upsetting about this or what did you like about it? … You might say it's stupid, this touchy-feely [stuff], but it's actually important for this population. Because a lot of them have so many hang-ups about math that it's very validating to hear someone else say that they found it confusing or they were embarrassed that they didn't understand negative numbers. And that let's a lot of them kind of let go - and actually open up and start to take a risk and think about these things for the first time.
The other thing is that all mathematicians know that we make mistakes constantly. When we're doing our professional work in research, we're constantly saying stupid things, making mistakes, correcting each other, being embarrassed. Your face gets red. That's normal. I mean, that's why they call it trial and error. You have to take risks, and try things, and make mistakes to make progress.
When we're doing our professional work in research, we're constantly saying stupid things, making mistakes, correcting each other, being embarrassed. Your face gets red. That's normal. I mean, that's why they call it trial and error. You have to take risks, and try things, and make mistakes to make progress.
But so much of school is, "Don't make any mistakes, get it right." This class, I feel, is a necessary corrective to that to show, that this is a safe place where you can make all the mistakes you want as long as you can learn from them. And it's fine and it's actually good because mistakes are very instructive.
There's a problem with this class, which is that we don't cover very much. And I'm not teaching any preestablished body of material that we have to get through. You can say, fine, you can get away with this because this is the last [math] class these students are ever going to take - and how much math did they really learn? OK, those are fair questions. But the things that they did learn they learned really well. And more than that, they learned what it actually means to do math, honestly, for the first time.
Because until then, they didn't know what math was. They were doing something else that's taught in school that's not real math. Just like being a trained monkey, honestly. It's just like, can you do the tricks that you're supposed to do. I know that's super-cynical to say, but ... for most people that's what a lot of their math experience is. "I'm supposed to solve this quadratic equation. OK, I'm going to see if I can factor it, and if I can't factor it, I'm going to use the quadratic formula. And I have no idea what I'm doing or why I care." That's what so many people go through.
Holodny: That's why they hate math.
Strogatz: That's why they hate it! No one wants to feel like a trained monkey.
Some of my colleagues are really skeptical. They're like, "Come on, what did they really learn in this course that they couldn't do before?" Well, actually they can do quite a bit that they couldn't do before, such as come up with their own arguments, but also explain them and understand why they're true.
I feel like they made a lot of progress. A lot of it changed their attitude quite a bit, which is a great thing to see. That they said, "I get why people love math. I never understood that before. And it is fun. And it makes me want to learn more" - which is the best of all.
Holodny: Aside from math, you're a great writer. How do you see the relationship between math and writing?
Strogatz: Math and writing - well, they feel to me like pretty different enterprises in many ways, but a part of them that feels quite similar is the need for organized thinking. That is, when people say that someone is a good writer, often what they mean is that he or she is a good thinker. Part of good writing is that the organization is good, one idea leads to the next, or a story flows naturally from what came before. The coherence of good writing is like the coherence of a good mathematical argument. You're not left wondering, why are we doing this now? That there's a natural flow when things are set up right. And it's hard to get them that way; that's what makes it difficult.
But then, as I hear myself saying all of that, about organized thinking in both writing and math, I also realize that they're both also similar in that you have to make a mess. You don't start out by doing organized thinking in either writing or math. You first start out by making a big mess in both - at least most people do - because you don't know where you're going with it.
To do something creative or very original, you will make a mess, you will break things, you'll be confused, you'll be sloppy, you'll try stuff that turns out to be a dead end. Whether it's a sentence or a paragraph or a calculation. That is common, I think, to all kinds of creative activities. That you have to be strong enough and brave enough to make a mess and to get stuck and to not give up.
To do something creative or very original, you will make a mess, you will break things, you'll be confused, you'll be sloppy, you'll try stuff that turns out to be a dead end ... You have to be strong enough and brave enough to make a mess and to get stuck and to not give up.
That's another thing that we don't teach enough in math - or in writing, probably - that the first draft is supposed to be terrible. Just get a first draft. I have a lot of trouble with this, I would admit. My wife, who's an artist, said to me that the way I write would be like if I were painting with the smallest brush. Like, I'm painting it all the details, trying to put the commas in the right place, and not thinking enough about the overall structure, the overall architecture of whatever I'm trying to do. And she said, and of course anyone knows this, that you have to paint first with the big brush, get the overall shape, and don't fill in the details until towards the end. You don't know where you're going, how can you possibly do it?
A similar thing with students trying to come up with a proof or derive an equation. They often are trying to do it step by step, and it doesn't work like that. You have to see the overall picture, which draws on a different part of the brain - intuition, visualization, some daring. And, by the way, social activity. We often mischaracterize math as this isolated and solitary endeavor, and it's not. A lot of math involves two people or more batting ideas around and arguing, trying to understand each other. It's social. That also can be messy, but that's how a lot of creative work is done.
Math and writing do have a lot of overlap in that they require these two facets of creativity. The first is the willingness to make a mess, and then the willingness to clean it up.
Read Steven Strogatz's book, "Joy of X: A Guided Tour of Math, from One to Infinity."

